Objective

1. เพื่อศึกษาคุณสมบัติของ Linear filter
2. เพื่อศึกษาความแตกต่างระหว่าง Linear filter
3. ศึกษาการประยุกต์ใช้ filter ในด้านการแพทย์

Medthods

1. Moving Average Filter

   Filter ชนิดนี้คือการสร้าง Mask สี่เหลี่ยมจัตุรัสขึ้นมา จากนั้นทำการเฉลี่ยค่าใน Mask เช่น หากสร้าง Mask ขนาด 3x3 ก็จะนำค่าทุกจุดใน Mask ซึ่งมีจำนวน 9 จุด มาเฉลี่ยกันและได้ค่าใหม่ โดยในที่นี้ได้ใช้ฟังก์ชั่น myWindow() ในการสร้าง Mask ซึ่งสามารถกำหนดขนาดได้ โดยฟังก์ชั่นนี้จะทำงานโดยการใส่อินพุดเป็นไฟล์ภาพเข้าไปจากนั้น จะเริ่มทำการสร้าง Mask และวิ่งไปบนภาพ จากนั้นจะ return ค่าเป็น Cell String ของทุกๆจุดที่วิ่งไป เมื่อได้ออกมาแล้วเราก็ทำการเฉลี่ยค่าในแต่ละหน้าต่างที่ได้ และได้ภาพใหม่ที่ผ่านการ Filter

   วิธีการสร้าง filter คือสร้าง matrix M ขนาดเท่ากับ mask หรือ window ที่ต้องการโดยมีผลรวมค่าต่างๆใน matrix เป็น 0 \(\sum^{M}_{i=1}{\sum^{N}_{j=1} M_{i,j}} = 1\) เพื่อให้ค่าที่ได้มีค่าน้อยกว่าหรือเท่ากับค่าเดิม (Gain = 1) จากนั้นนำรูปภาพ A ที่ต้องการใส่ filter Convolution กับ M ผลลัพท์ที่ได้จะเป็นภาพที่มี filter ตามที่ต้องการ

   $$\begin{split} \psi_{M,N} &= \frac{1}{MN} \begin{pmatrix}1 & 1 & \cdots & 1\\1 & 1 & \cdots & 1\\ \vdots & \vdots & \ddots & \vdots \\ 1 & 1 & \cdots & 1 \end{pmatrix} \\ Output &= A \ast \Psi\end{split}$$ เมื่อ A เป็น matrix 2 มิติของภาพใดๆ \(\Psi_{M,N}\) เป็น window ขนาด \(M \times N \)

2. Properties of Linear Filter

   1. 2.1 scale preservation คือการปรับเปลี่ยนค่าโดยการนำค่าคงที่ไปกระทำกับ function หรือ นอก function จะให้ค่าผลลัพธ์เดียวกัน ดังนี้ \(L(\alpha X) = \alpha L(X)\)
   2. 2.2 Superposition คือ การเปลี่ยนแปลงค่าด้วยคุณสมบัติการกระจาย ซึ่งผลลัพธ์ที่ได้จะมีค่าเท่ากัน ดังคุณสมบัตินี้ \(L(X_{1} + X_{2}) = L(X_{1}) + L(X_{2})\)
   3. 2.3 Time invariance คือคุณสมบัติในการปรับ scale ซึ่งคุญสมบัตินี้เหมือนกับ scale presevation ดังนั้นผลลัพธ์ที่ได้จะเหมือนกัน ดังสมการนี้ \(L(B^{kX}) = B^{kL(X)}\)

   คุณสมบัติทั้งสามข้อจะทำให้เราสามารถแยกชนิดของ filter ว่าเป็น linear filter หรือ non-linear filter ซึ่งคุณสมบัติทั้งสามนี้ เราสามารถทำให้เป็นสมการรูปแบบที่ง่าย คือ \(y = mx + c\) ซึ่งเป็นสมการเส้นตรง

3. Offset and Scaling Filter

   การทำ Filter ชนิดนี้จะคล้ายกับการทำ Moving Average Filter ต่างกันเพียง Filter ชนิดนี้จะเพิ่มการปรับ contrast ของภาพเข้าไปด้วย โดยการใช้ประโยชน์จากคุณสมบัติ Linear filter ซึ่งทำให้เราสามารถ ปรับค่า brightness และ contrast ก่อนหรือหลังจากการใส่ filter

   $$L(aX + b) = aL(X) + b$$เมื่อ L คือ Linear filter X คือภาพที่นำเข้า a และ b เป็นค่าคงที่ใด

   ในที่นี่จะใช้ฟังก์ชั่น myFilter() ซึ่งฟังก์ชั่นนี้จะเป็นการทำ Moving Window Average และทำการปรับ contrast ของภาพเรียบร้อย และได้เอาท์พุดออกมาเป็นภาพใหม่ที่ผ่านการ filter และปรับ contrast แล้ว

   

   

4. Gaussian Filter

   Gaussain filter เป็น local operation ในการเปลี่ยนแปลงค่าของ pixel ในภาพโดยเอาค่า pixel จากพื้นที่ใกล้เคียงมาทำการ operation ซึ่ง Gaussian filter จะนำรูปแบบ normal distribution มาประยุกต์ใช้ในการ filter ภาพที่มี Gaussian noise เป็น noise ที่เกิดขึ้นภายในภาพ ซึ่งจะทำหน้าที่ทำให้ภาพ smooth หรือ blur ดังตัวอย่างภาพใน result นอกจากนี้ ยังทำหน้าที่เป็น low pass filter ซึ่งการปรับเปลี่ยนค่าของ filter ขึ้นอยู่กับขนาดของ mask และ sigma ของ normal distribution

   $$\begin{split} \psi(x,y) &= e^{-(x^2+y^2) \over 2\sigma^2} \end{split}$$

   $$ \begin{split} \Psi_{M,N} &= \begin{pmatrix} \psi(-\frac{M}{2},-\frac{N}{2}) & \psi(-\frac{M}{2},-\frac{N}{2}+1) & \cdots & \psi(-\frac{M}{2},\frac{N}{2}) \\ \psi(-\frac{M}{2}+1,-\frac{N}{2}) & \psi(-\frac{M}{2}+1,-\frac{N}{2}+1) & \cdots & \psi(-\frac{M}{2}+1,\psi(-\frac{M}{2},\frac{N}{2})) \\ \vdots & \vdots & \ddots & \vdots \\ \psi(\frac{M}{2},-\frac{N}{2}) & \psi(\frac{M}{2},-\frac{N}{2}+1) & \cdots & \psi(\frac{M}{2},\psi(-\frac{M}{2},\frac{N}{2}))\\ \end{pmatrix}\\ Output &= A \ast \Psi \end{split} $$ เมื่อ A เป็น matrix 2 มิติของภาพใดๆ \(\Psi_{M,N}\) เป็น window ขนาด \(M \times N \)

   

5. Mexican Hat Filter

   Mexican Hat filter เป็น local operation รูปแบบหนึ่งที่ใช้ในการ edge detection จะทำหน้าที่เป็น high pass filter และเรียกอีกอย่างหนึ่งว่า laplace filter ช่วยทำให้ภาพคมชัดมากยิ่งขึ้น หลักการทำงานของ filter ชนิดนี้เหมือนกับ gaussian filter ซึ่งมีพารามิเตอร์ sigma เป็นการปรับความละเอียดของภาพ ยิ่งค่า sigma สูงจะทำให้ภาพเบลอยิ่งขึ้น [1]

   $$\begin{split} \psi(x) &=(1-x^{2})e^{-x^{2}/2} \\ \psi(x,y) &= [1-(x^{2}+y^{2})]e^{-\frac{x^{2}+y^{2}}{2}}\\ \psi(x,y) &= {2 \over {\sqrt {3\sigma}\pi^{1 \over 4}}} \left( 1 - {x^2+y^2 \over \sigma^2} \right) e^{-(x^2+y^2) \over 2\sigma^2} \end{split}$$

   $$ \begin{split} \Psi_{M,N} &= \begin{pmatrix} \psi(-\frac{M}{2},-\frac{N}{2}) & \psi(-\frac{M}{2},-\frac{N}{2}+1) & \cdots & \psi(-\frac{M}{2},\frac{N}{2}) \\ \psi(-\frac{M}{2}+1,-\frac{N}{2}) & \psi(-\frac{M}{2}+1,-\frac{N}{2}+1) & \cdots & \psi(-\frac{M}{2}+1,\psi(-\frac{M}{2},\frac{N}{2})) \\ \vdots & \vdots & \ddots & \vdots \\ \psi(\frac{M}{2},-\frac{N}{2}) & \psi(\frac{M}{2},-\frac{N}{2}+1) & \cdots & \psi(\frac{M}{2},\psi(-\frac{M}{2},\frac{N}{2}))\\ \end{pmatrix}\\ Output &= A \ast \Psi \end{split} $$ เมื่อ A เป็น matrix 2 มิติของภาพใดๆ \(\Psi_{M,N}\) เป็น window ขนาด \(M \times N \)

   

Results

จากการศึกษา Moving Window AverageFilter และ การปรับ Contrast ทางกลุ่มได้ทำการเขียนฟังก์ชั่นการทำงานบนโปรแกรม MATLAB และได้ผลออกมาเป็นดังภาพด้านล่าง

1. JPEG Image

   

2. LSM

   

3. DICOM

   

4. Linear Filter บน AVI Video

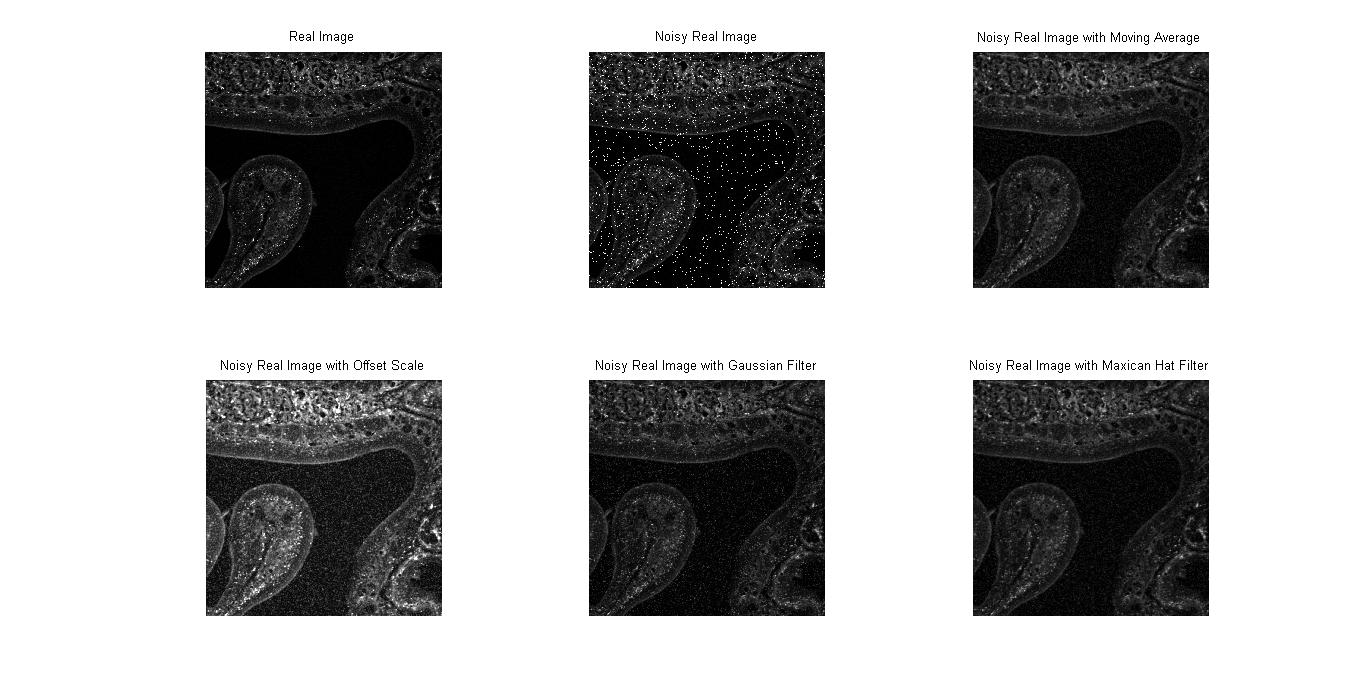
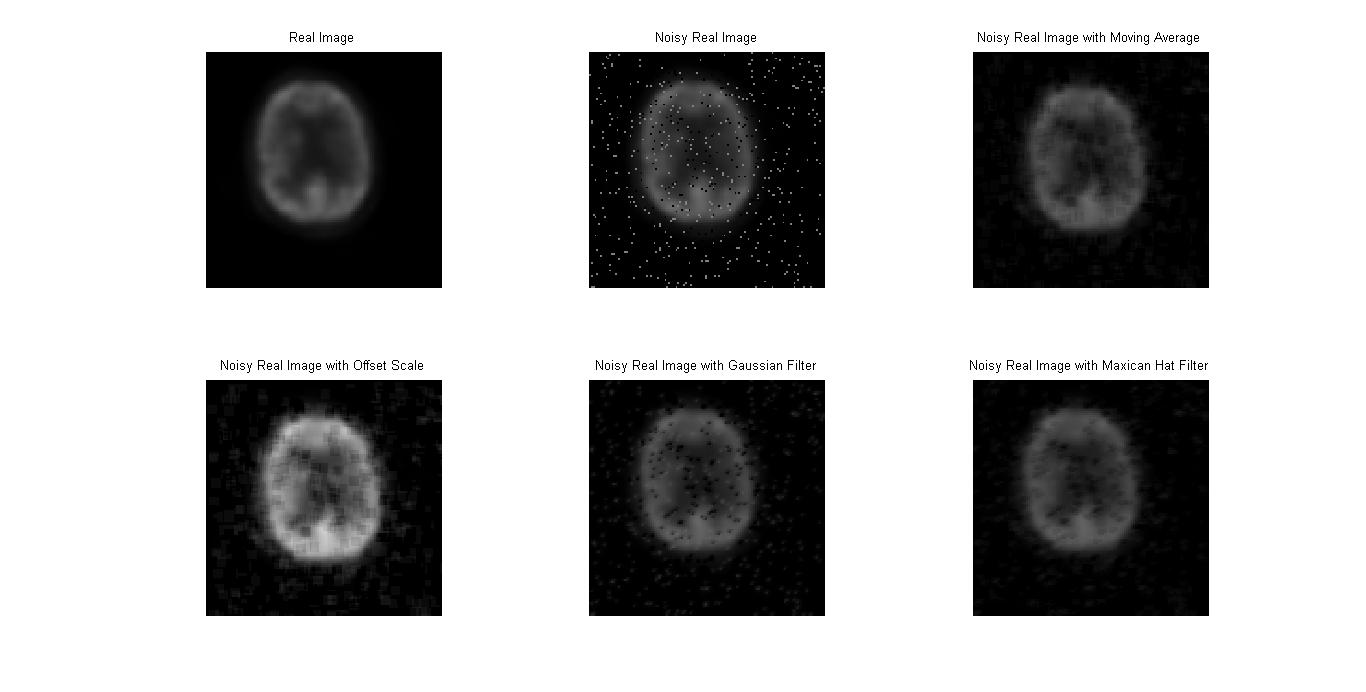
   เรียงจาก

   • Raw Video
   • Moving Average filter window=3x3
   • Gaussian filter sigma และ window เพิ่มขึ้นเรื่อยๆ
   • Mexican hat filter sigma = 1.1 window = 3x3
   • Mexican hat filter sigma = 1.8 window = 5x5

   Video แสดง filter แบบต่างๆ

5. Linear Filter บนภาพจาก Webcam

   Video แสดงผลการประมวลผลภาพจากกล้อง webcam ประกอบไปด้วยภาพต้นแบบ (บนซ้าย) ภาพจากการทำ moving average filter ขนาด 5x5 (A) ภาพการทำ Gaussian blur \(\sigma = 1\) ขนาด 5x5 (B) ภาพการทำ Mexican hat filter \(\sigma = 1.8\) ขนาด 5x5 (C)

Discussion

จากการทดลองใช้ filter ทั้งสามชนิดโดยการเซตค่าพารามิเตอร์เพื่อดูการเปลี่ยนแปลงของภาพที่เกิดขึ้นหลังการ filter โดยใช้ convolution mask 5x5 เป็นการเซตค่าmask เพราะมันมีผลต่อการfilter ยิ่งmask ขนาดเล็กยิ่งมีความละเอียดสูงมากกว่าขนาดใหญ่ ซึ่งขนาดใหญ่จะทำให้ภาพสูญเสียรายละเอียดของภาพไป พารามิเตอร์ที่ใช้ในการปรับภาพ คือ scale การเพิ่มด้วยการคูณ และ การบวกลบของค่า offset การปรับ filter แบบนี้ผลที่ได้คือการปรับค่าความสว่างของ pixel ค่าบวกความสว่างก็จะเพิ่มขึ้นเป็นต้น การปรับพารามิเตอร์ที่ใช้กับ gaussian และ mexican hat filter คือค่าของ sigmaจะเป็นค่าของการ smooth ที่จะทำให้ภาพเบลอขึ้น ยิ่งปรับค่า sigma เพิ่มขึ้นภาพก็จะเบลมากขึ้นจนรายละเอียดภาพเสียหาย เป็นต้น ดังนั้นสรุปได้ว่า ค่าพารามิเตอร์ที่ใช้ในการทดลองมีผลต่อการ filter ภาพที่เกิดขึ้นในทิศทางเดียวกัน

Conclusion and Future Study

การประยุกต์ใช้ linear filter มีทั้งข้อดีและข้อเสียในการจัดการกับภาพที่เราต้องการ filter ดังนั้นเราต้องศึกษา filter เพื่อใช้้งานให้เหมาะสมที่สุดและมีความละเอียดที่ดีที่สุดสำหรับการ filterภาพ และควรจะเพิ่มฟังก์ชั่นเสริมที่สามารถตกแต่งภาพหลังจากการถูกfilter เช่น contrast scale

จากการศึกษา linear filter มาประยุกต์ใช้กับภาพทางการแพทย์ ซึ่งการเลือกใช้ filter แต่ละชนิดขึ้นกับความต้องการของผู้ใช้ว่าต้องการให้ภาพออกมาแบบไหนถึงจะชัดเจนที่สุด สำหรับ linear filter มีข้อจำกัดในการคำนวน convolution mask เราต้องการปรับเปลี่ยน mask ให้มีความละเอียดยิ่งขึ้น เช่น asymetric mask ในการประยุกต์ใช้เพื่อลดการเสียหายของภาพที่เกิดจากการ filter นอกจากนี้ เราต้องการศึกษาเพิ่มเติมเกี่ยวกับ non linear filter มาประยุกต์ใช้กับภาพในอนาคต

Q&A

Question 1:

Noise ในภาพคืออะไร และสามารถเกิดขึ้นได้อย่างไร

Answer:

Noise เป็นสัญญานรบกวนที่เกิดขึ้นในภาพ ทำให้เห็นความไม่สม่ำเสอของความสว่างและสี สามารถเกิดขึ้นได้จาก

1. จำนวณ photon ที่ตกลงในแต่ละ pixel ที่ต่างกัน
2. ความสามารถในการสร้างประจุของ photo diode แตกต่างกัน
3. สัญญานรบกวนในการส่งผ่านข้อมูลอิเล็กทรอนิกส์

Question 2:

จงบอกข้อดีและข้อเสียของ moving average filter

Answer:

ข้อดีของ moving average filter คือ ช่วยลด random noise ในช่วง sharp step response ซึ่งได้ดีใน spartial domain

ข้อเสียคือ moving average filter คือเป็น filter ที่สามารถทำงานได้แย่ใน frequency domain เนื่องจากความสามารถในการแยก band of frequency จาก frequency อื่นๆนั่นต่ำมาก

Question 3:

หากใช้ Multiple-pass moving average filters มากกว่า 4 ครั้ง ผลที่ได้จะเป็นอย่างไร

Answer:

ผลที่ได้จะเหมือนกับการใช้ Gaussian filter mask

References

[1] Guo, H., Q. He, and B. Jiang. The Application of Mexican Hat Wavelet Filtering and Averaging Algorithm in Raman Spectra Denoising. in Image and Signal Processing, 2008. CISP '08. Congress on. 2008.

[3] Image Processing Toolbox, User Guide, Version 4. [2003], The MathWorks, Inc., Natick, MA.

[4] Using MATLAB, Versoin 6.5 [2002], The MathWorks, Inc., Natick, MA.

All source code available on Github