Objective

1. เพื่อศึกษาความหมายของ hit, fit และ miss ใน Morphological Filter
2. เพื่อศึกษาความแตกต่างของ mask แต่ละรูปแบบ
3. เพื่อศึกษาการทำงานและความแตกต่างของ Erosion และ Dilation
4. เพื่อเปรียบเทียบประสิทธิภาพระหว่าง Function ที่สร้างขึ้นเองกับ Function ใน MATLAB Toolbox
5. เพื่อศึกษาการประยุกต์ใช้ Morphological Filter ในด้านการแพทย์

Medthods

1. Hit, Fit, and Miss

   Hit - บริเวณที่ structuring elementตัดกับส่วนใดส่วนหนึ่งของpixel บนรูปภาพ โดยจะเป็นไปตามสัญลักษณ์ \(\left \{ y:y=x+s,s\in S \right \}\subset I \)โดยหมายถึง S hits I ที่ x

   Fit - บริเวณที่ structuring elementครอบทับทุกส่วนของpixel บนรูปภาพ โดยจะเป็นไปตามสัญลักษณ์ \(\left \{ y:y=x-s,s\in S \right \}\cap I\neq \oslash \) โดยหมายถึง S fits I ที่ x

   Miss - บริเวณที่ structuring elementไม่ตัดกับส่วนใดส่วนหนึ่งของpixel บนรูปภาพ โดยจะเป็นไปตามสัญลักษณ์ \(\left \{ y:y=x-s,s\in S \right \}\cap I= \oslash\) โดยหมายถึง S misses I ที่ x โดยภาพด้านล่างจะแสดง hit, miss และ fit ของภาพที่ได้จาก structuring element ที่กำหนด

   

2. Structuring Elements

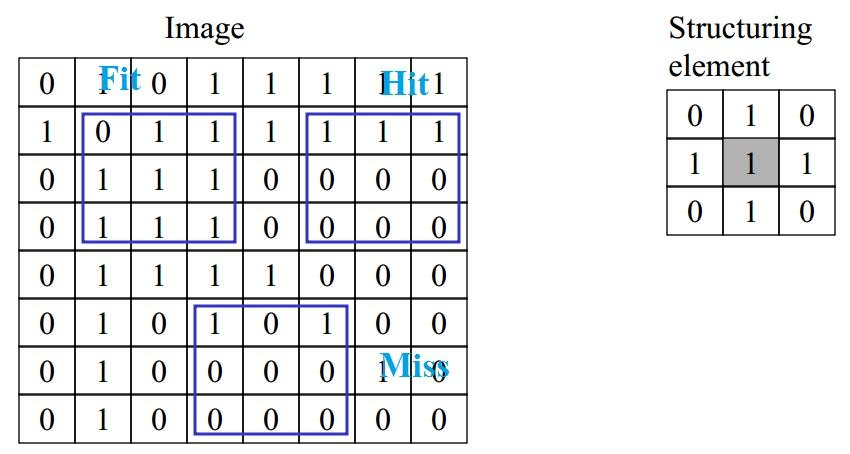
   ในบทนี้เราได้สร้าง structuring element เป็น 4 แบบ คือ circle, diamond, donut และ square

   • square มีการสร้างเป็นสี่เหลี่ยมจัตุรัสโดยรับ input เป็นค่าความยาวหรือความกว้างของสี่เหลี่ยม

   • diamond เป็นการสร้างสี่เหลี่ยมจัตุรัสที่มีลักษณะคล้ายเพชรขึ้นมา โดยรับ input เป็นระยะห่างระหว่างจุดศูนย์กลางถึงมุม (\(r\)) โดย matrix ของ structuring element นี้จะเป็นไปตามสมการ \(x + y <= r\)

   • circle เป็นการส้รางวงกลมขึ้นมาโดยฟังก์ชั่นจะรับค่าเป็นรัศมีของวงกลม จากนั้นจะสร้างวงกลมด้วยสมการวงกลม คือ \( (x-x_2)^2+(y-y_2)^2 <= r^2 \) โดยที่ \(x_2\) และ \(y_2\) เป็นพิกัดของ origin ของวงกลม

   • donut ป็นการสร้างวงกลมที่มีรูเป็นวงกลมตรงกลาง โดยจะ input ค่าเข้าไปเป็นรัศมีของวงกลมวงใหญ่และวงเล็ก โดยใช้ฟังก์ชั่นของ circle ด้านบนในการสร้าง structuring element นี้

3. Dilation

   Dilation เป็นวิธีการขยายภาพโดยจะเป็นการเพิ่มจำนวน pixel บนภาพโดยจะเป็นไปตามสัญลักษณ์ $$ A\oplus B = \left \{ x \mid (B)_x\cap A\neq \oslash \right \} $$ โดยที่ B เป็น structuring element หากจะอธิบาอย่างง่ายก็คือ การดู pixel แต่ละ pixel ของภาพ หากมีค่าเป็น 0 ก็จะไม่เกิดอะไรขึ้น แต่หากจุดนั้นมีค่าเป็น 1 ก็จะนำ origin ของ structurin element ไปวางบน pixel นั้น เช่น ให้ $$ A = \begin{bmatrix}1 &0 &0 &0 &1 \\ 0 &1 &0 &0 &1 \\ 0 &0 &0 &0 &0 \\ 0 &0 &1 &0 &1 \\ 0 &0 &0 &0 &0 \end{bmatrix} $$ และให้ $$ B = \begin{bmatrix}0 &1 &0 \\ 1 &1 &1 \\ 0 &1 &0 \end{bmatrix} $$ จะได้ภาพใหม่เป็น $$ \begin{bmatrix}1 &1 &0 &1 &1 \\ 1 &1 &1 &1 &1 \\ 0 &1 &1 &0 &1 \\ 0 &1 &1 &1 &1 \\0 &0 &1 &0 &1 \end{bmatrix} $$

4. Erosion

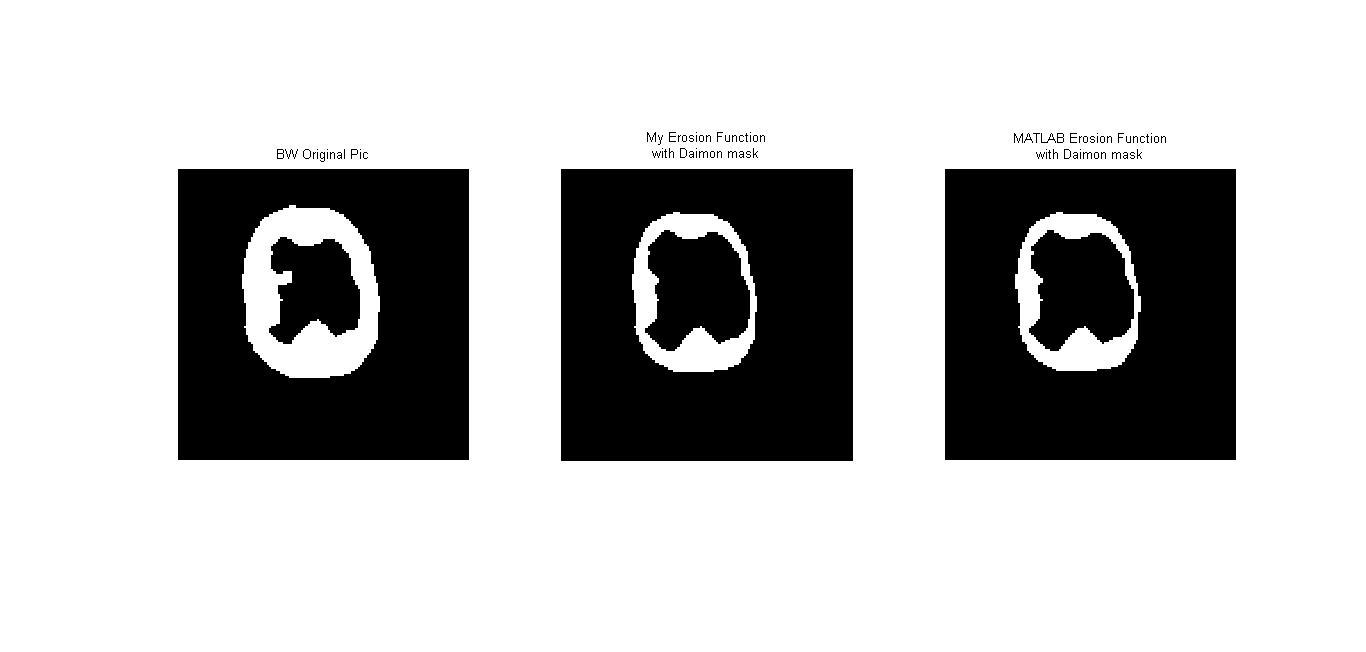
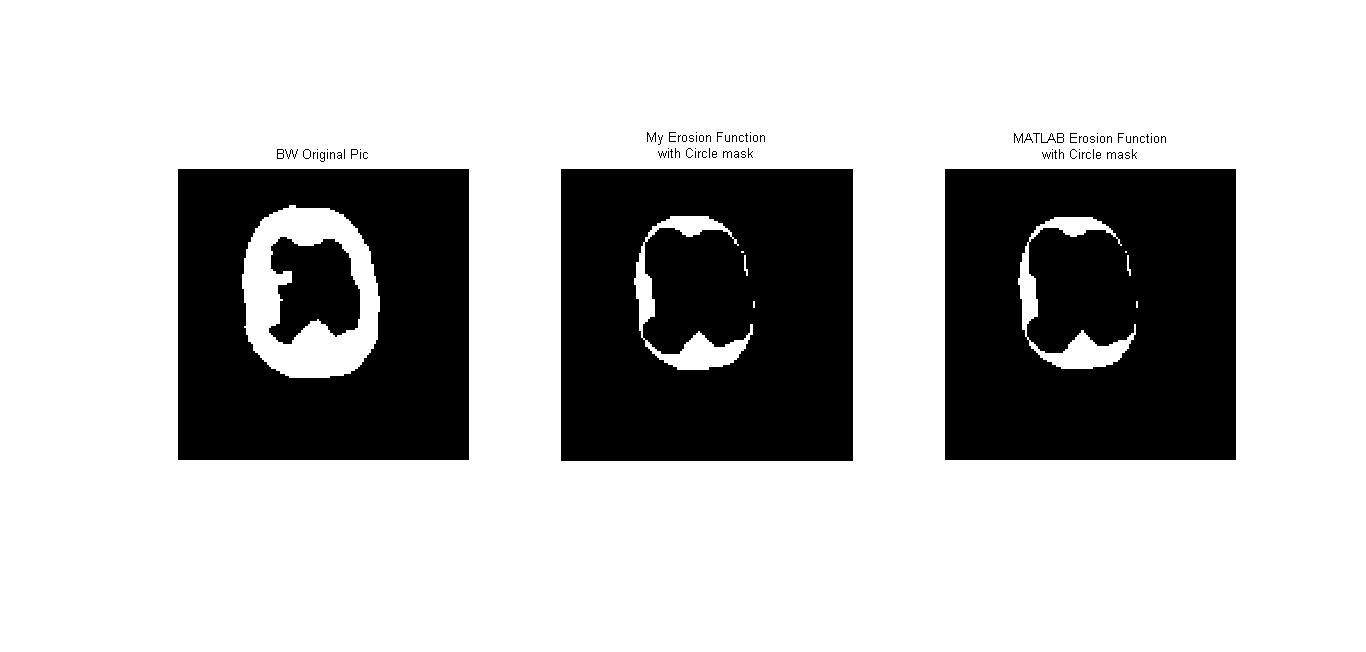
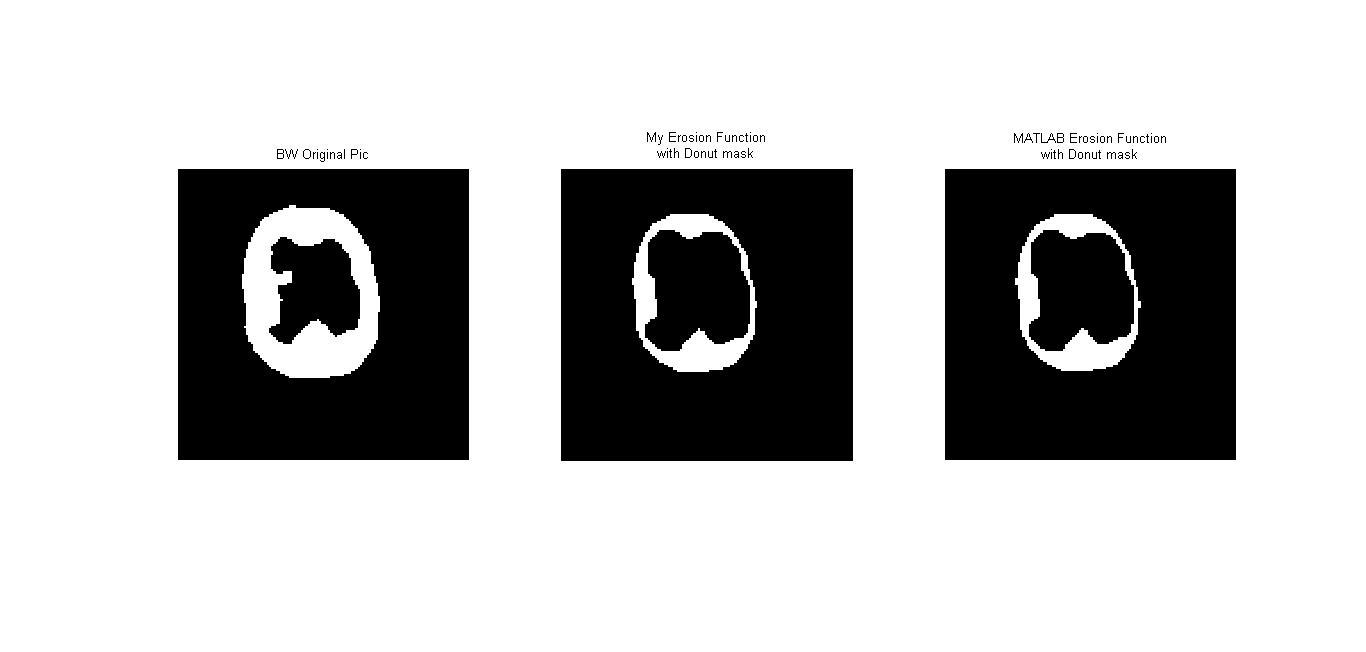
   Erosion เป็นวิธีการย่อภาพโดยจะทำการลบ pixel ที่ขอบของภาพออก โดยจะเป็นไปตามสัญลักษณ์ $$ A \ominus B = \left\{ x \mid (B)_x\subseteq A \right\} $$ โดยที่ A เป็นภาพ และ B เป็น structuring element หากจะอธิบายอย่างง่ายก็คือ การนำจุด origin ของ structuring element ไปวางที่ pixel ภาพที่สนใจ และหากทุกจุดที่เป็น 1 บน structuring element เหมือนกับบนภาพ เราจะให้ pixel นั้นบนภพมีค่าเป็น 1 แต่หากไม่ใช่ จะให้จุดนั้นมีค่าเป็น 0 เช่น หากให้ภาพ $$A = \begin{bmatrix}1 &0 &0 &0 &1 \\ 0 &1 &1 &0 &1 \\ 1 &1 &1 &1 &0 \\ 1 &1 &1 &0 &1 \\ 1 &1 &1 &1 &1 \end{bmatrix} $$ และ structuring element $$B = \begin{bmatrix}0 &1 &0 \\ 1 &1 &1 \\ 0 &1 &0 \end{bmatrix}$$ เมื่อทำการ erosion จะได้ภาพใหม่คือ $$\begin{bmatrix}0 &0 &0 &0 &0 \\ 0 &0 &0 &0 &0 \\ 0 &1 &1 &0 &0 \\ 0 &1 &0 &0 &0 \\ 0 &0 &0 &0 &0 \end{bmatrix}$$

Results

1. JPEG (Coin.jpg)

   

   

   

   

   

   

   

   

2. DICOM

   

   

   

   

   

   

   

   

3. LSM

   

   

   

   

   

   

   

   

4. AVI video

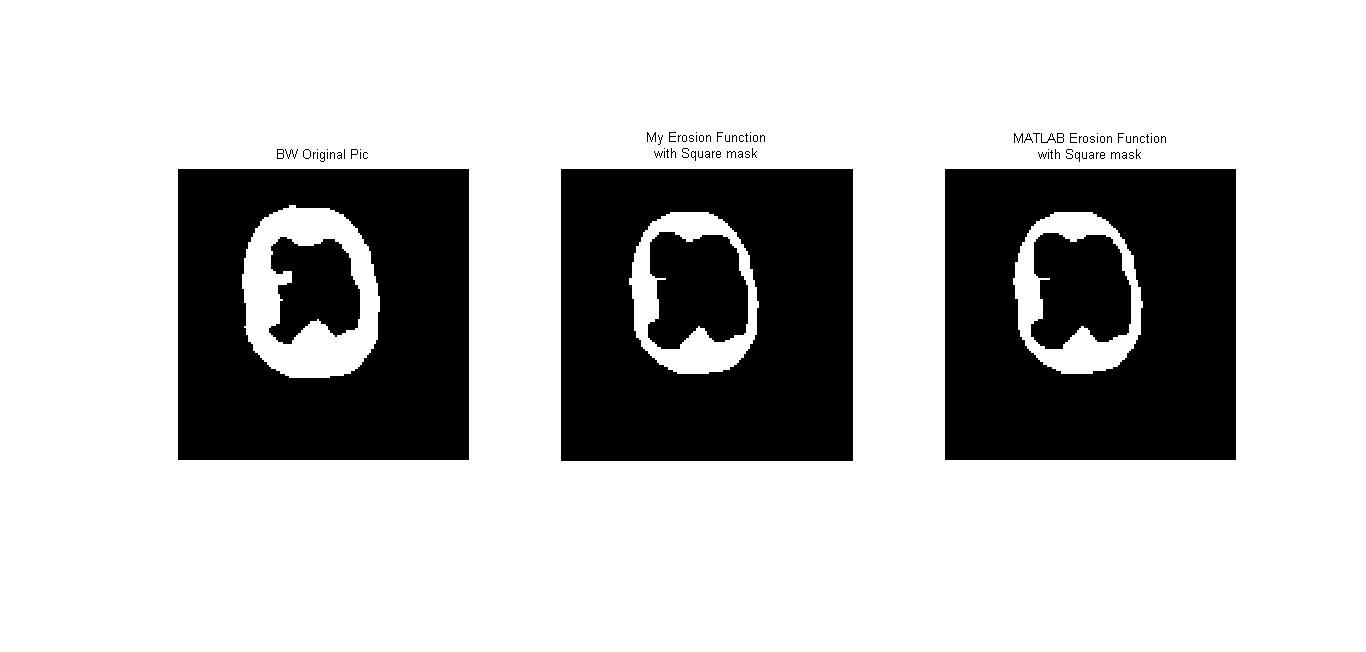
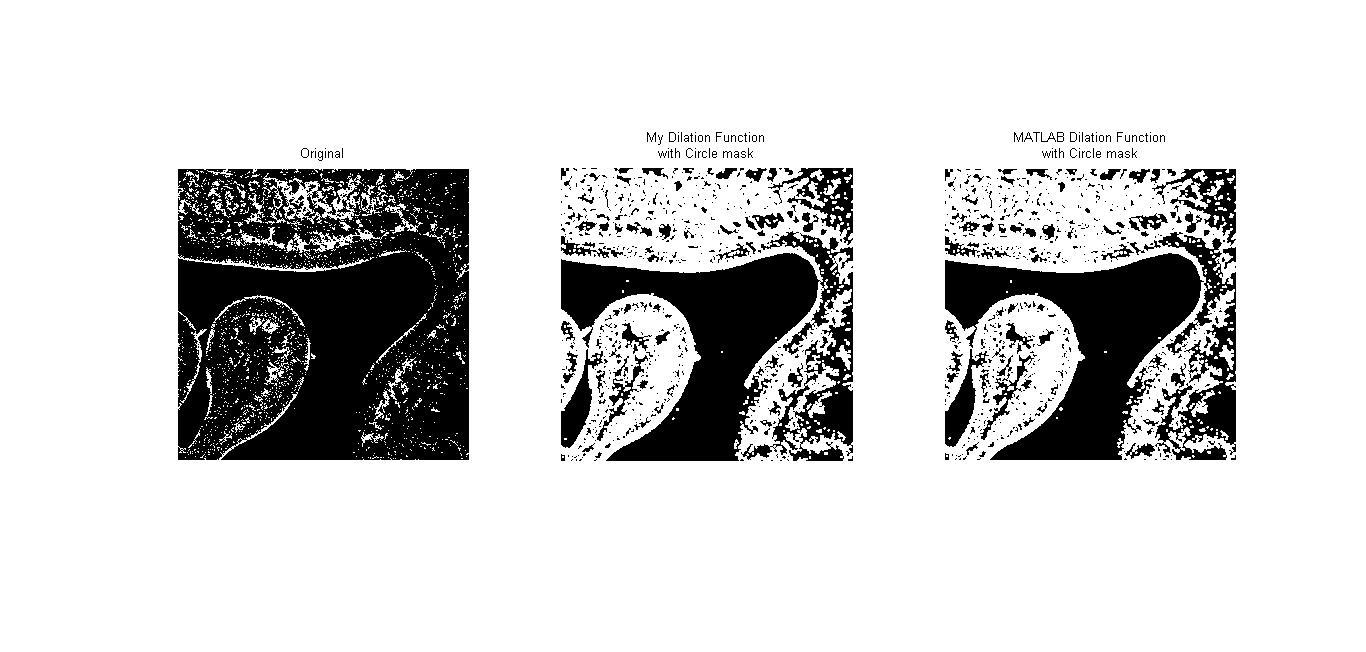
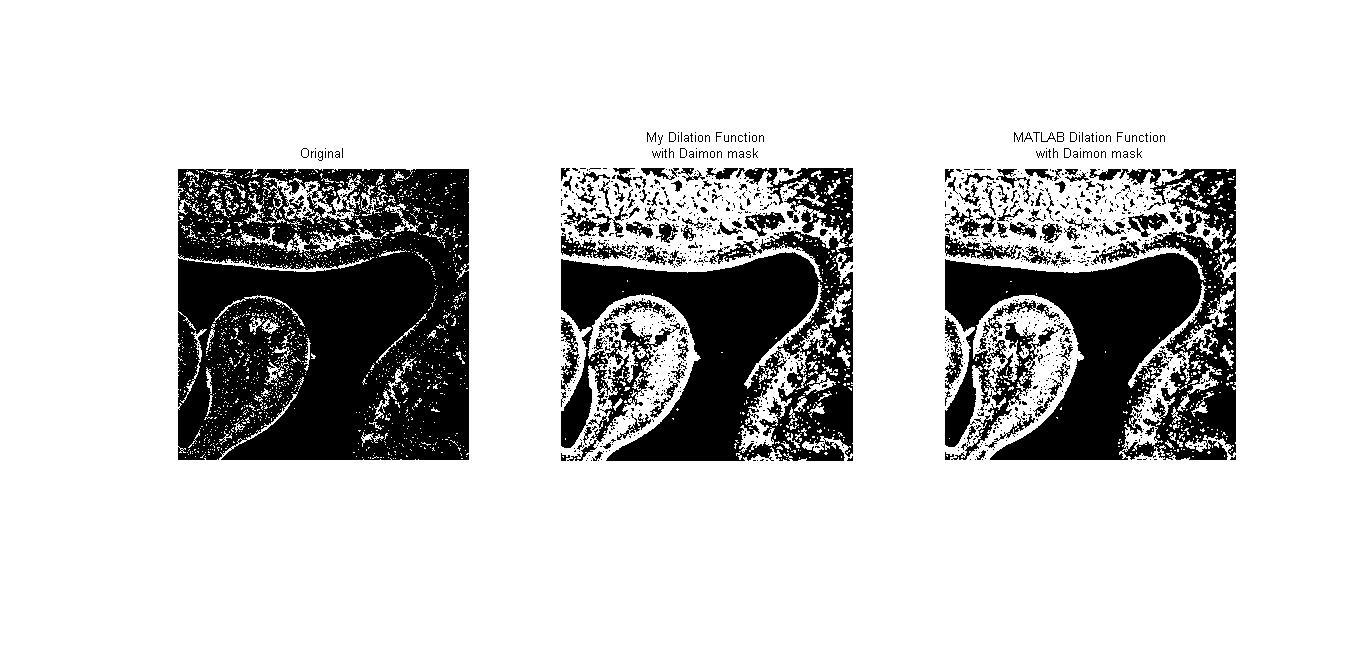
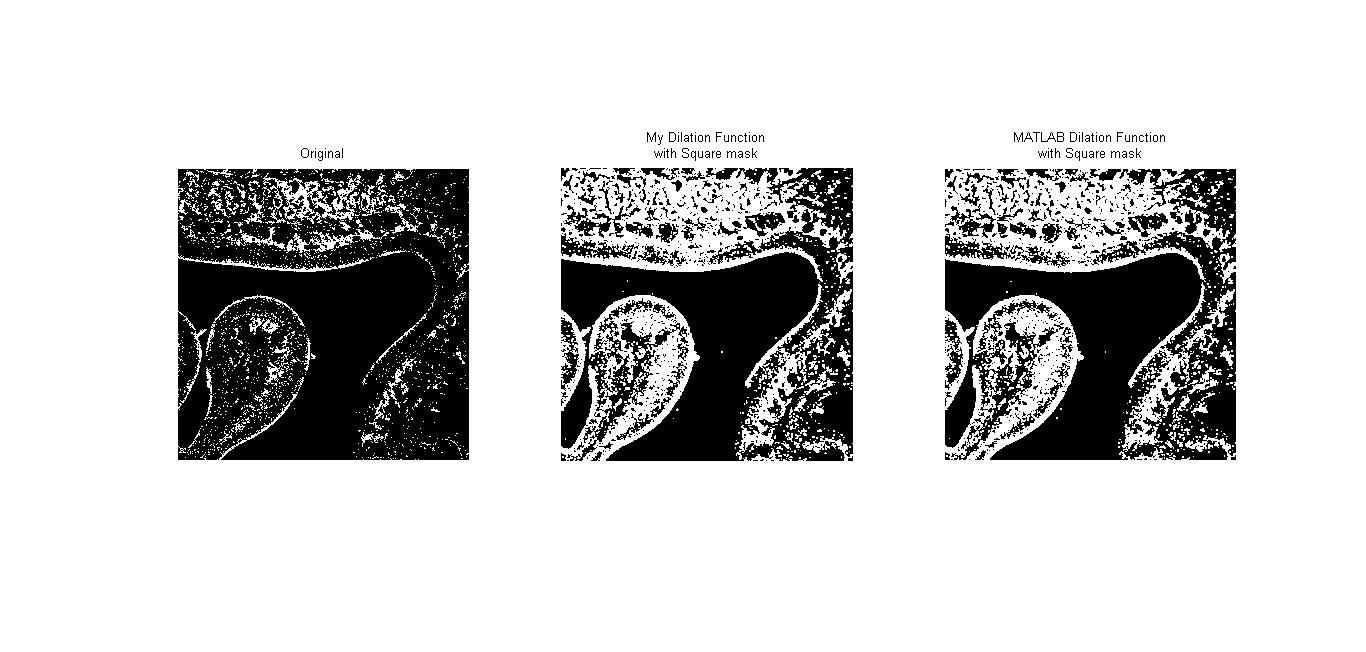
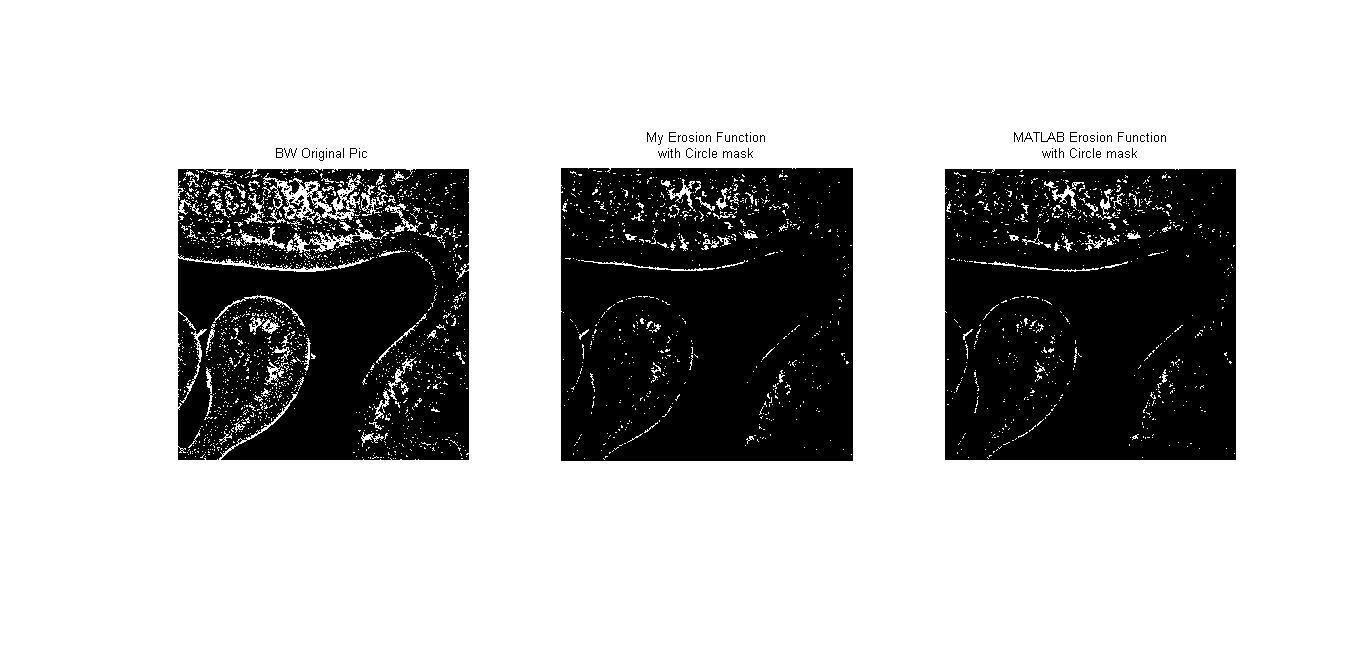
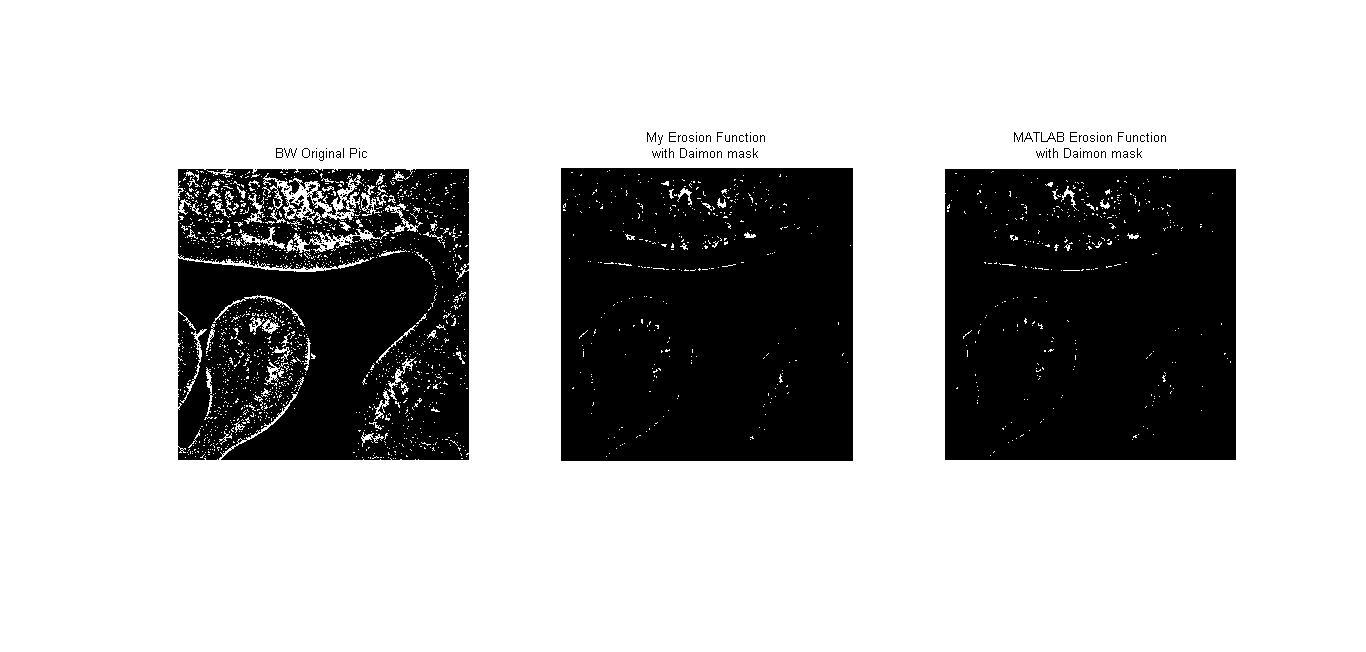
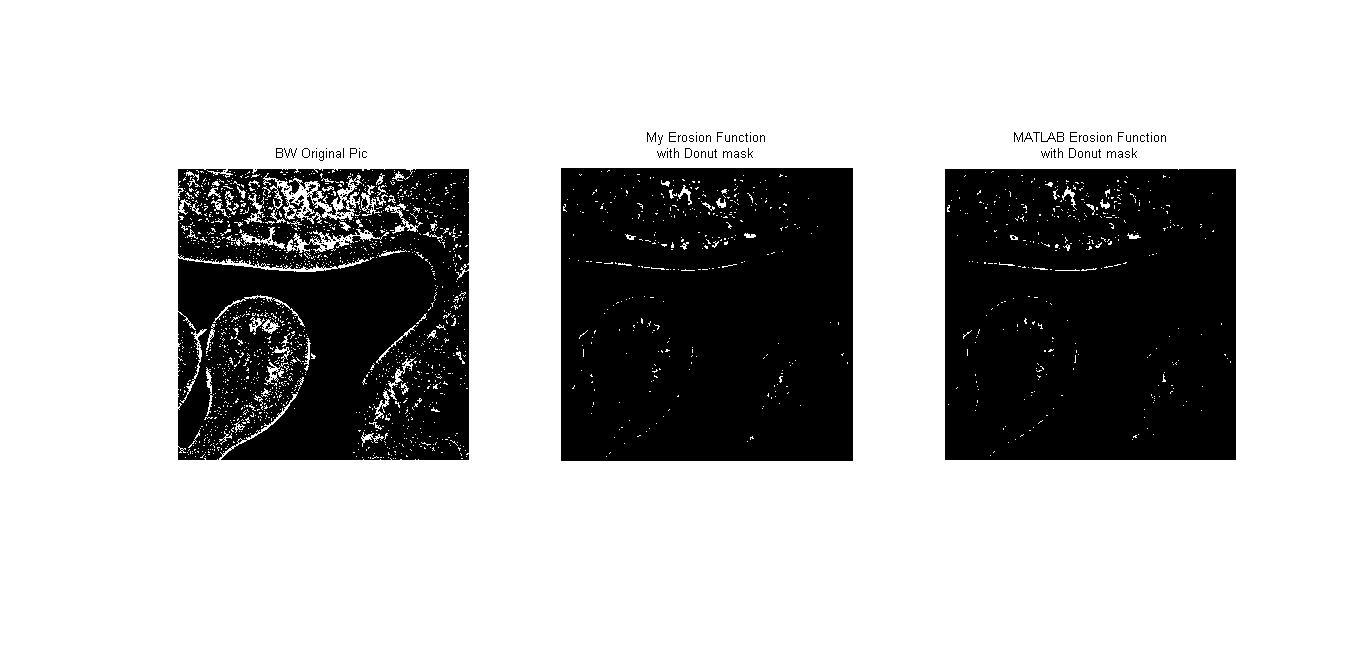
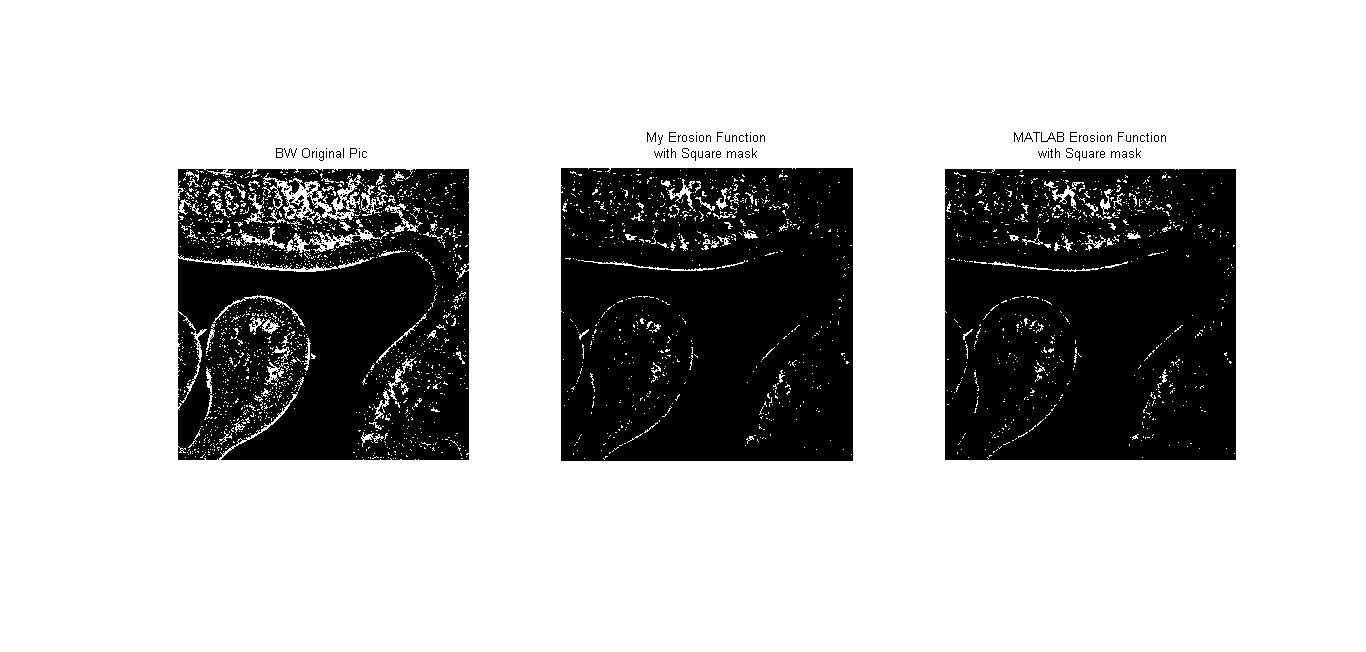
   Video 1 : แสดงผลการประมวลผลภาพจาก AVI file แสดงผลการทำ Dilation ด้วยการผ่าน Structuring Element แบบต่างๆ

   Video 2 : แสดงผลการประมวลผลภาพจาก AVI file แสดงผลการทำ Erosion ด้วยการผ่าน Structuring Element แบบต่างๆ

5. Webcam

   Video 3 : แสดงผลการประมวลผลภาพจากกล้อง webcam แสดงผลการทำ Dilation ด้วยการผ่าน Structuring Element แบบต่างๆ

   Video 4 : แสดงผลการประมวลผลภาพจากกล้อง webcam แสดงผลการทำ Erosion ด้วยการผ่าน Structuring Element แบบต่างๆ

Conclusion

วิธีการ Morphogical เป็นการปรับปรุงภาพที่เป็นแบบขาวดำ หรือ BWโดยวิธีการ Dilation และ Erosion จะทำให้ภาพมีความแตกต่างกัน โดย Dilation จะเป็นการขยายภาพให้มีขนาดใหญ่ขึ้นและอาจมีการอุดรูหรือลดขนาดรูที่เกินขึ้นในภาพ แต่ Erosion นั้นจะเป็นการลดขนาดภาพจากขอบของภาพหรืออาจจะลบ pixel ที่อาจะเป็น noise ในภาพออก จะเห็นได้ดัง Results ที่้ผ่านมา และนอกจากนี้การทำ Dlation และ Erosion นั้น ภาพที่ได้ก็ยังขึ้นอยู่กับ structuring element ทั้งชนิดของ structuring element หรือขนาดของมัน โดยหากมีขนาดใหญ่ ภาพที่ไต้ก็จะมีการขยายมากหรือมีการลดขนาดมากกว่าภาพที่ใช้ structuring element ขนาดเล็ก

Discussion

ในการทำ Erosion และ Dilation สามารถนำไปใช้ในการปรับปรุงภาพถ่ายได้ โดยจะต้องทำการศึกษาวิธีการในขั้นต่อๆไปโดยจะเป็นการใช้ทั้ง Dilation และ Erosion ทั้งคู่ในการปรับปรุงภาพ และการเลือกใช้ structuring element ทั้งชนิดและขนาดก็ส่งผลต่อภาพได้ ดังนั้นจึงควรเลือกใช้ structuring element ให้เหมาะสม เช่น หากทำ Erosion ด้วย structuring element ที่มีขนาดใหญ่เกินไปก็อาจะทำให้ภาพสูญเสียรายละเอียดมากเกินไป ภาพใหม่ที่ได้ก็อาจมีการผิดเพี้ยนไป

Future Study

จากการที่ทางกลุ่มได้ทำการศึกษาเกี่ยวกับ Morphological filter ที่ใช้ใน image procrssing ครั้งนี้ สามารถนำไปประยุกต์ใช้กับภาพที่มี pixel สูงหรือต่ำเกินไป จนไม่สามารถมองเห็นภาพที่แท้จริงได้ Morphological filter จะช่วยให้ภาพนั้นๆชัดเจนเด่นชัด เห็นเป็นรูปเป็นร่างขึ้นมา เพียงแต่ในครั้งนี้จะเป็นการใช้งานเบื้องต้น จะมีการใช้งานที่ซับซ้อนและได้ผลดีในครั้งต่อไป

Q&A

Question 1:

จงยกตัวอย่าง fundamental operation ที่เกี่ยวเนื่องกับ morphological filter

Answer:

union, intersection, complement และ translation

Question 2:

Minkowski sum คืออะไร มีความสัมพันธ์อย่างไรกับ morphological filter

Answer:

Minkowski sum หรือ addition ของ 2 เซตระหว่างเซต A และ B เป็น vector addition ของ แต่ละ element ใน A กับแต่ละ element ของ B $$ A \oplus B = \left\{ \mathbf{a+b} \mid \mathbf{a} \in A, \mathbf{b} \in B \right\} $$ ซึ่งสัมพันธ์กันกับ dilation ของเซต A โดยเซต B ซึ่ง B คือ structuring element เช่น $$ \begin{split} A &= \left\{ (1, 0), (0, 1), (0, -1) \right\} \\ B &= \left\{ (0, 0), (1, 1), (1, -1) \right\} \\ A \oplus B &= \left\{ (1, 0), (2, 1), (2, −1), (0, 1), (1, 2), (1, 0), (0, −1), (1, 0), (1, −2) \right\}  \end{split} $$

Question 3:

จงบอกผลลัพท์ที่แตกต่างกันระหว่างการทำ opening และ closing

Answer:

opening จะเป็นการ smooth จากด้านในของ object contour แต่ closing จะเป็นการ smooth จากด้านนอกของ object contour

References

1. G.Brostow. 2008. Morphological Operations. Slides in class GV12/3072 (Image Processing). Computer Science Department University College London. availbled from: http://www0.cs.ucl.ac.uk/staff/G.Brostow/classes/IP2008/L3_Morphology.pdf

Source code is available on Github